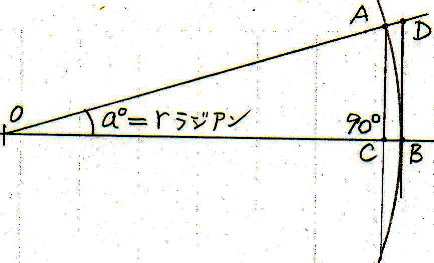微小角の三角関数の応用(08-03-24)
下の図でABは半径1の円の円弧です。この円弧の長さはAOBで作る角の角度a°に比例するので角度の表示に使うことができます。
この方法での角度の表現法が一つラジアン表示です。
下の図でABはおOを中心とする円弧とし、OA=OB=1とすれば
円弧AB長さで角度aをあらわします。
半径1の円の円周は2π,円周角は360°の関係があるので
r:a°=2π:360° r=a°*2π/360°
です。
QAC、ODBは何れも直角三角形でOA=OB=1ですから
CA=sin(r)、BD=tan(r)の関係が成立します。
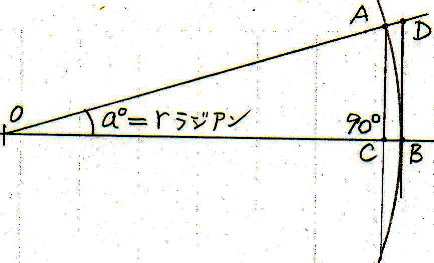
角度aが「微小」のとき
sin(r)≒tan(r)≒r
cos(r)≒1-r^2/2
の関係が成立するのを微小角の三角関数の近似といいます。これは上の図で直線CA、円弧AB、直線BDの長さがほぼ同じことである程度納得できます。
微小とはどの位小さい角か?が問題ですが実際は結構大きい角でもこの近似関係は成立します。下の表でr/sとt/rはsin(r)とtan(r)をrラジアンで近似した場合の誤差です。例えば20°の場合の誤差はsinで2.1%、tanで4.3%で模型設計には許容できる数字です。
この「微小」角の三角関数は角度の簡易計算にも応用できます。
| 度: a |
ラジアン: r |
sin: s |
tan: t |
r/s |
t/r |
cos |
1-r^2/2 |
| 0.0° |
0.000 |
0.000 |
0.000 |
|
|
1.000 |
1.000 |
| 1.0° |
0.017 |
0.017 |
0.017 |
1.000 |
1.000 |
1.000 |
1.000 |
| 2.0° |
0.035 |
0.035 |
0.035 |
1.000 |
1.000 |
0.999 |
0.999 |
| 3.0° |
0.052 |
0.052 |
0.052 |
1.000 |
1.001 |
0.999 |
0.999 |
| 4.0° |
0.070 |
0.070 |
0.070 |
1.001 |
1.002 |
0.998 |
0.998 |
| 5.0° |
0.087 |
0.087 |
0.087 |
1.001 |
1.003 |
0.996 |
0.996 |
| 6.0° |
0.105 |
0.105 |
0.105 |
1.002 |
1.004 |
0.995 |
0.995 |
| 7.0° |
0.122 |
0.122 |
0.123 |
1.002 |
1.005 |
0.993 |
0.993 |
| 8.0° |
0.140 |
0.139 |
0.141 |
1.003 |
1.007 |
0.990 |
0.990 |
| 9.0° |
0.157 |
0.156 |
0.158 |
1.004 |
1.008 |
0.988 |
0.988 |
| 10.0° |
0.175 |
0.174 |
0.176 |
1.005 |
1.010 |
0.985 |
0.985 |
| 12.5° |
0.218 |
0.216 |
0.222 |
1.008 |
1.016 |
0.976 |
0.976 |
| 15.0° |
0.262 |
0.259 |
0.268 |
1.012 |
1.023 |
0.966 |
0.966 |
| 17.5° |
0.305 |
0.301 |
0.315 |
1.016 |
1.032 |
0.954 |
0.953 |
| 20.0° |
0.349 |
0.342 |
0.364 |
1.021 |
1.043 |
0.940 |
0.939 |
| 22.5° |
0.393 |
0.383 |
0.414 |
1.026 |
1.055 |
0.924 |
0.923 |
| 25.0° |
0.436 |
0.423 |
0.466 |
1.032 |
1.069 |
0.906 |
0.905 |
| 27.5° |
0.480 |
0.462 |
0.521 |
1.039 |
1.085 |
0.887 |
0.885 |
| 30.0° |
0.524 |
0.500 |
0.577 |
1.047 |
1.103 |
0.866 |
0.863 |
ゴム動力模型飛行機ホームページ
模型航空力学資料・資料関連リンク